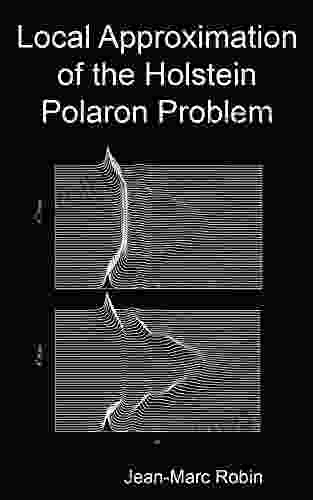
Local Approximation of the Holstein Polaron Problem: A Comprehensive Guide

The Holstein polaron problem is a classic problem in solid-state physics that describes the interaction between an electron and phonons (quantized lattice vibrations) in a crystal lattice. This interaction can lead to the formation of a polaron, which is a quasiparticle consisting of an electron dressed by a cloud of phonons.
5 out of 5
| Language | : | English |
| File size | : | 2350 KB |
| Screen Reader | : | Supported |
| Print length | : | 156 pages |
| Lending | : | Enabled |
The local approximation is a simplified method for treating the electron-phonon interaction in the Holstein polaron problem. In this approximation, the electron-phonon interaction is treated as a local interaction, which means that it is assumed to only affect the electron's motion within a small region of the crystal lattice.
The local approximation can be used to derive a number of important properties of the Holstein polaron. For example, it can be used to calculate the polaron's effective mass, which is the mass of the polaron as it moves through the crystal lattice. The local approximation can also be used to calculate the polaron's mobility, which is the polaron's ability to move through the crystal lattice.
The local approximation is a powerful tool for understanding the Holstein polaron problem. However, it is important to note that the local approximation is only a simplified model of the electron-phonon interaction. In some cases, the local approximation may not be accurate, and more sophisticated methods may be needed to treat the electron-phonon interaction.
Applications of the Local Approximation
The local approximation has been used to study a number of different physical systems, including:
- Polarons in semiconductors
- Polarons in metals
- Polarons in insulators
- Polarons in organic materials
The local approximation has also been used to study a number of different physical phenomena, including:
- Polaron transport
- Polaron scattering
- Polaron relaxation
- Polaron formation
The local approximation is a powerful tool for understanding the Holstein polaron problem. It is a simple and computationally efficient method that can be used to derive a number of important properties of the Holstein polaron. However, it is important to note that the local approximation is only a simplified model of the electron-phonon interaction, and in some cases, more sophisticated methods may be needed to treat the electron-phonon interaction.
References
- Holstein, T. (1959). Studies of polaron motion. Part I. The molecular-crystal model. Annals of Physics, 8, 325-342.
- Devreese, J. T., & Alexandrov, A. S. (2009). Fröhlich polaron and bipolaron: recent developments. Reports on Progress in Physics, 72(6),066501.
- Alexandrov, A. S., & Devreese, J. T. (2010). Advances in polaron physics. Springer Science & Business Media.
5 out of 5
| Language | : | English |
| File size | : | 2350 KB |
| Screen Reader | : | Supported |
| Print length | : | 156 pages |
| Lending | : | Enabled |
Do you want to contribute by writing guest posts on this blog?
Please contact us and send us a resume of previous articles that you have written.
 Book
Book Novel
Novel Page
Page Chapter
Chapter Text
Text Story
Story Genre
Genre Reader
Reader Library
Library Paperback
Paperback E-book
E-book Magazine
Magazine Newspaper
Newspaper Paragraph
Paragraph Sentence
Sentence Bookmark
Bookmark Shelf
Shelf Glossary
Glossary Bibliography
Bibliography Foreword
Foreword Preface
Preface Synopsis
Synopsis Annotation
Annotation Footnote
Footnote Manuscript
Manuscript Scroll
Scroll Codex
Codex Tome
Tome Bestseller
Bestseller Classics
Classics Library card
Library card Narrative
Narrative Biography
Biography Autobiography
Autobiography Memoir
Memoir Reference
Reference Encyclopedia
Encyclopedia Steve Turner
Steve Turner Eric C Lindstrom
Eric C Lindstrom Kathy Valentine
Kathy Valentine Eric Butterworth
Eric Butterworth Mira Jacob
Mira Jacob Leah Mcgrath Goodman
Leah Mcgrath Goodman Marilynn Reynolds
Marilynn Reynolds Glenn Berkenkamp
Glenn Berkenkamp Marion I Tobler Rohr
Marion I Tobler Rohr Fred Luskin
Fred Luskin Sajni Patel
Sajni Patel Ian V Rowe
Ian V Rowe Trevor Clinger
Trevor Clinger Gary R Kremer
Gary R Kremer Shawn Bean
Shawn Bean Eric Flanagan
Eric Flanagan Kenneth Ma
Kenneth Ma William Egelman
William Egelman Lorna Stuber
Lorna Stuber Eric Van Lustbader
Eric Van Lustbader
Light bulbAdvertise smarter! Our strategic ad space ensures maximum exposure. Reserve your spot today!

 Jeffrey HayesUnlock the Power of Animation Storytelling: Immerse Yourself in the Digital...
Jeffrey HayesUnlock the Power of Animation Storytelling: Immerse Yourself in the Digital...
 Hamilton BellThe Essential Guide to Planning a Baby Shower: A Comprehensive Handbook for...
Hamilton BellThe Essential Guide to Planning a Baby Shower: A Comprehensive Handbook for... Rubén DaríoFollow ·18.9k
Rubén DaríoFollow ·18.9k Holden BellFollow ·5k
Holden BellFollow ·5k Peter CarterFollow ·12.9k
Peter CarterFollow ·12.9k Gil TurnerFollow ·12.4k
Gil TurnerFollow ·12.4k Arthur MasonFollow ·2.4k
Arthur MasonFollow ·2.4k Anton FosterFollow ·17.2k
Anton FosterFollow ·17.2k Darren NelsonFollow ·15.7k
Darren NelsonFollow ·15.7k Wayne CarterFollow ·19k
Wayne CarterFollow ·19k

 Roland Hayes
Roland HayesMagda: A Mother's Love, A Daughter's Redemption - A...
Immerse Yourself in the Captivating True Story...

 Spencer Powell
Spencer PowellSnow White Retold: A Tale of Love, Magic, and...
Once upon a time, in...
 Jake Powell
Jake PowellMaster the SATs with Effective Strategies from 99th...
The SATs are a challenging exam,...

 Brian Bell
Brian BellSEO for Dummies: Unlock the Secrets to Search Engine...
In today's digital...

 Jaylen Mitchell
Jaylen MitchellBechtel: Unveiling the Unsung Heroes Who Built the World
In the annals of global infrastructure, the...
5 out of 5
| Language | : | English |
| File size | : | 2350 KB |
| Screen Reader | : | Supported |
| Print length | : | 156 pages |
| Lending | : | Enabled |